Sensitivities of portfolios are typically computed by banks every day. These are used for P&L risk management, hedging purposed, VaR calculations and its associated regulatory capital, etc.
In this paper, Chebyshev Tensors are used to compute dynamic sensitivities of financial instruments within a Monte Carlo simulation. Dynamic sensitivities are then used to compute Dynamic Initial Margin as defined by ISDA (SIMM), to a high degree of accuracy and low computational cost. The technique is benchmarked against the computation of dynamic sensitivities obtained by using pricing functions as found in risk engines.
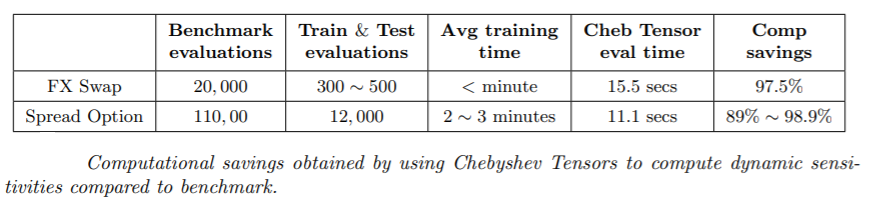
Numerical tests were done on FX swaps and Spread Options, where the technique obtains high accuracy at different percentiles of the simulated distributions with substantial computational gains over the benchmark.
The benchmark computation for dynamic sensitivities was obtained by calling the pricing function at each node of the simulation. Computational gains stand at 97.5% for the FX swap and between 89% and 98.9% for the Spread Option, and can be applied to wide range of trade types.
The key element is the dimension of the tensor to build. In CCR (counterparty credit risk), most of the models used have a dimension that the Tensor Extension Algorithms can handle. Problems can appear in cases such as Basket Options with a large number of underlyings modeled independently. However, for a typical portfolio, the researchers expect the technique to apply for the vast majority of live and newly incoming trades.

