Researchers from the University of Freiberg and NTU Singapore study pricing and hedging under parameter uncertainty for a class of Markov processes which they call generalized affine processes and which includes the Black-Scholes model as well as the constant elasticity of variance (CEV) model as special cases.
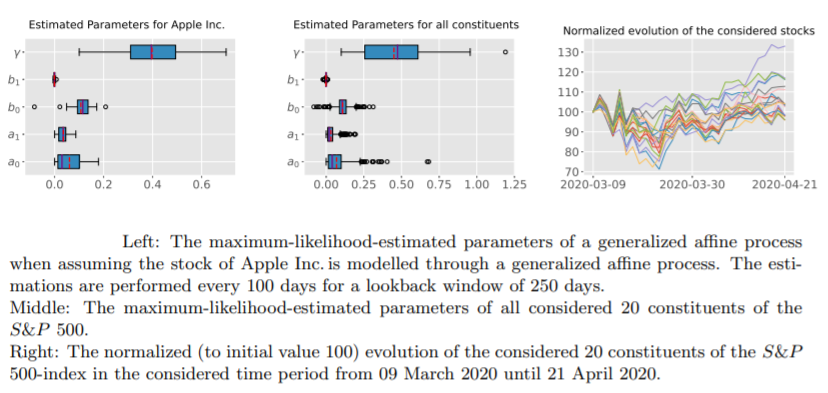
For a realistic data application, researchers consider the COVID-19 period, when stock markets experienced unexpectedly high volatility and variation in the price paths, which poses a huge challenge to classical hedging approaches.
Based on a general dynamic programming principle, researchers are able to link the associated nonlinear expectation to a variational form of the Kolmogorov equation which opens the door for fast numerical pricing in the robust framework. The main novelty of the paper is that they propose a deep hedging approach which efficiently solves the hedging problem under parameter uncertainty. They numerically evaluate this method on simulated and real data and show that the robust deep hedging outperforms existing hedging approaches, in particular in highly volatile periods.